| Каталог документации / Раздел "Базы данных, SQL" | (Архив | Для печати) |
| ||
Хранение иерархических данных (или попросту — деревьев) в реляционных структурах задача довольно нетривиальная и вызывает некоторые проблемы, когда разработчики сталкиваются с подобной задачей.
В первую очередь, это связано с тем, что реляционные базы не приспособлены к хранению иерархических структур (как, например, XML-файлы), структура реляционных таблиц представляет из себя простые списки. Иерархические же данные имеют связь родитель-наследники, которая не реализована в реляционной структуре.
Тем не менее, задача хранить деревья в базе данных рано или поздно возникает перед любым разработчиком.
Ниже мы подробно рассмотрим, какие существуют подходы в организации хранения деревьев в реляционных БД, а также рассмотрим инструментарий, который нам предоставляет ORM Doctrine для работы с такими структурами.
Как правило, такая структура данных предполагает хранение информации о смежных вершинах нашего дерева. Давайте рассмотрим простейший граф с темя вершинами (1,2,3):
Рис. 1. Граф с тремя вершинами
Как видим каждый элемент данного графа хранит информацию о связи с другими элементами, т.е.:
1 - 2,3 2 - 1,3 3 - 1,2
Фактически, для построения дерева такой граф избыточен, т.к. для привычной ветвистой структуры нам нужно хранить только связь родитель-наследник, т.е.:
2-1 3-1
Тогда мы получим дерево с одним корневым элементом (1) и двумя ветками (2,3):
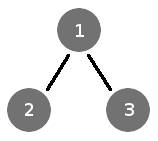
Рис. 2. Граф дерева
В принципе, тот и другой графы можно, при желании, отобразить в базе данных с помощью списка смежных вершин, но, поскольку нас интересуют именно деревья, остановимся на них.
Итак, чтобы хранить в базе данных иерархическую структуру методом списка смежных вершин (Adjacency List), нам необходимо хранить информацию о связях наследник-родитель в таблицах с данными. Давайте рассмотрим реальный пример дерева:
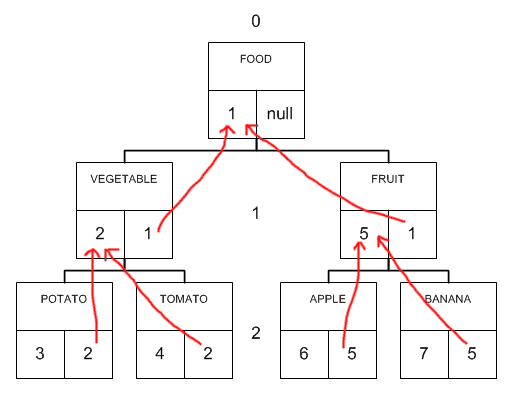
Рис. 3. Древовидная структура методом смежных вершин
На рисунке квадратами обозначены узлы деревьев. У каждого узла есть имя (верхний прямоугольник внутри квадрата), идентификатор (левый нижний квадрат) и ссылка на идентификатор родителя (правый нижний квадрат). Как видно из Рис. 3, каждый наследник в такой структуре ссылается на своего предка. В терминах БД мы можем это отобразить следующим образом в виде таблицы:

Рис. 4. Таблица данных дерева, построенная методом списка смежных вершин
Или же в виде SQL:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | CREATE TABLE al_tree ( `id` BIGINT NOT NULL AUTO_INCREMENT PRIMARY KEY, `parent_id` BIGINT NULL, `name` VARCHAR(50) NOT NULL ) TYPE=InnoDB DEFAULT CHARSET=utf8; CREATE INDEX fk_tree_tree ON al_tree (parent_id); ALTER TABLE al_tree ADD CONSTRAINT fk_tree_tree FOREIGN KEY (parent_id) REFERENCES al_tree (id) ON UPDATE CASCADE ON DELETE CASCADE; INSERT INTO al_tree VALUES (1, NULL, 'FOOD'), (2, 1, 'VEGETABLE'), (3, 2, 'POTATO'), (4, 2, 'TOMATO'), (5, 1, 'FRUIT'), (6, 5, 'APPLE'), (7, 5, 'BANANA'); |
Следует сразу отметить, что такой алгоритм хранения деревьев обладает определенными как достоинствами, так и недостатками. В первую очередь, он не совсем удобен для чтения — и это его основной недостаток.
Проблемы с чтением из БД менее заметны, если вычитывать все дерево целиком. Это достаточно простой запрос:
1 | SELECT * FROM al_tree ORDER BY id; |
Результат:
+----+-----------+-----------+ | id | parent_id | name | +----+-----------+-----------+ | 1 | NULL | FOOD | | 2 | 1 | VEGETABLE | | 3 | 2 | POTATO | | 4 | 2 | TOMATO | | 5 | 1 | FRUIT | | 6 | 5 | APPLE | | 7 | 5 | BANANA | +----+-----------+-----------+
Однако в дальнейшем такая выборка подразумевает достаточно емкую программную пост-обработку данных. Сначала нужно рекурсивно перестроить данные с учетом связей предок-наследник и лишь потом их можно будет использовать для вывода куда-либо.
Другой вариант чтения дерева целиком:
1 2 3 4 5 6 | SELECT t1.name AS lvl1, t2.name as lvl2, t3.name as lvl3 FROM al_tree AS t1 LEFT JOIN al_tree AS t2 ON t2.parent_id = t1.id LEFT JOIN al_tree AS t3 ON t3.parent_id = t2.id LEFT JOIN al_tree AS t4 ON t4.parent_id = t3.id WHERE t1.id = 1; |
Результат в данном случае будет такой:
+------+-----------+--------+ | lvl1 | lvl2 | lvl3 | +------+-----------+--------+ | FOOD | VEGETABLE | POTATO | | FOOD | VEGETABLE | TOMATO | | FOOD | FRUIT | APPLE | | FOOD | FRUIT | BANANA | +------+-----------+--------+
Хотя данные в таком виде уже более приспособлены сразу для вывода, но, как видите, главный недостаток такого подхода — необходимо достоверно знать количество уровней вложенности в вашей иерархии, кроме того, чем больше иерархия, тем больше JOIN'ов — тем ниже производительность.
Тем не менее, данный способ обладает и существенными достоинствами — в дерево легко вносить изменения, менять местами и удалять узлы.
Вывод — данный алгоритм хорошо применим, если вы оперируете с небольшими древовидными структурами, которые часто поддаются изменениям.
С другой стороны, этот алгоритм также довольно уверенно себя чувствует и с большими деревьями, если считывать их порциями вида знаю родителя — прочитать всех наследников. Хороший пример такого случая — динамически подгружаемые деревья. В этом случае алгоритм практически оптимизирован для такого поведения.
Однако он плохо применим, когда нужно вычитывать какие-либо иные куски дерева, находить пути, предыдущие и следующие узлы при обходе и вычитывать ветки дерева целиком (на всю глубину).
Сначала хотелось бы высказать несколько вводных слов по организации шаблонов таблиц в Doctrine, с помощью которых подобные вещи в ней и реализуются. Те, кто уже знаком с этой концепцией в доктрине, может перескочить несколько абзацев вперед к более интересным вещам.
Итак, сущности, которыми мы оперируем в ORM Doctrine — это активные записи. Т.е. объекты, которые совмещают в себе бизнес-логику и сами умеют взаимодействовать с базой данных. Но разработчики Doctrine предусмотрели расширение функциональности объектов записей не только наследованием, но и применением к этим объектам «шаблонов поведения». Это реализуется пакетом Doctrine/Template.
Т.о., если возникает необходимость воспитать активную запись до какого-либо поведения (например, Versionable — проводит аудит всех изменений, I18N — многоязычная или NestedSet — древовидная вида вложенное множество), то это можно сделать как раз с помощью данных шаблонов поведения.
Чтобы подключить какой-либо из существующих шаблонов, достаточно сконфигурировать должным образом нашу модель (посредством YAML или прямо в коде базовой таблицы модели).
Когда придет время, мы покажем на примерах, как это сделать.
Пока, к сожалению, или к счастью, но в виде шаблона к таблицам метод списка смежных вершин в Doctrine не реализован. При желании вы можете написать реализацию сами и даже предложить ее разработчикам Doctrine, — это уже на ваше усмотрение.
Тем не менее, основные функции, которые могут быть реализованы в рамках данной модели, можно реализовать в Doctrine и без использования шаблонов поведения. К сожалению, функций работы с деревом мы не получим, но основные задачи решать сможем.
Для этого следует сконфигурировать нашу модель должным образом. Используя YAML опишем структуру нашей таблицы:
1 2 3 4 5 6 7 8 9 10 11 | AlTree: tableName: al_tree columns: id: type: integer(8) primary: true autoincrement: true name: type: string(50) notnull: true parent_id: integer(8) |
А вот теперь самое важное — правильно описать связи в таблице. Там же со следующей строчки напишем:
1 2 3 4 5 6 7 8 9 10 11 | relations: Parent: class: AlTree local: parent_id foreign: id type: one Children: class: AlTree local: id foreign: parent_id type: many |
Теперь соберем нашу модель, запустив команду:
1 | ./doctrine generate-models-yaml |
Все. Модель готова. Фактически тоже самое можно было сделать в уже готовом базовом классе BaseAlTree:
1 2 3 4 5 6 7 8 9 10 | ... public function setUp() { $this->hasOne('AlTree as Parent', array('local' => 'parent_id', 'foreign' => 'id')); $this->hasMany('AlTree as Children', array('local' => 'id', 'foreign' => 'parent_id')); } ... |
Теперь пришло время насладиться результатами нашей работы. Напишем несложный код, отображающий дерево, построенное с отступами на обычной HTML-странице, используя рекурсию.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 | /** * Извлекаем корневой элемент дерева */ $root = Doctrine::getTable( 'AlTree')->findByDql( 'WHERE parent_id IS NULL')->getFirst(); echo '<pre>'; printRTree( $root); echo '</pre>'; /** * Рекурсивно печатет дерево на экран * * @param AlTree $node - объект записи - узел дерева * @param int $level - уровень вложенности переданого узла */ function printRTree( AlTree $node, $level = 0) { /** * Вот эта строчка и "рисует" наше дерево */ echo str_repeat( "\t", $level) . $node->getName() . "\n"; /** * Далее проверяем, есть ли наследники, * и если есть - входим в рекурсию. * Обратите внимание - вот то чудо-свойство * Children, которое мы описали в конфиге * нашей модели! */ if (($children = $node->Children->getIterator()) && $children->count() > 0) { $level++; while (($child = $children->current())) { /** * Входим в рекурсию */ printRTree( $child, $level); $children->next(); } } } |
Обратите внимание, после того, как мы сконфигурировали должным образом связи у нашего объекта модели, нам стали доступны свойства Children и Parent. Однако любое первое обращение к ним на чтение порождает запрос к базе данных. Поэтому, для построения больших деревьев целиком за один проход, такой подход может оказаться довольно затратным.
Но в тоже время, реализовать динамически подгружаемое дерево таким способом — одно удовольствие!
Об этом алгоритме и его быстродействии, наверное, слышали все веб-разработчики. Да, этот алгоритм действительно очень хорош, когда требуется часто и много обращаться к иерархическим данным на чтение. Рассмотрим суть данного подхода.
При построении дерева на основе вложенных множеств, мы воспользуемся принципом обхода этого дерева слева-направо, как показано стрелками на Рис. 5. Для этого определим для каждого узла дерева целочисленные ключи слева (lft) и справа (rgt) (нижние квадратики внутри узла). И раздадим им во время обхода целочисленные инкрементные значения. Посмотрите что получилось.
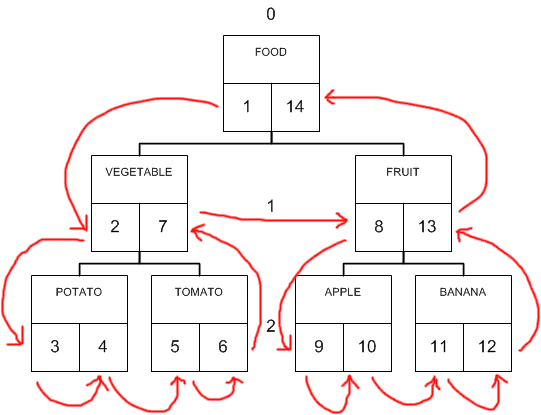
Рис. 5. Вложенное множество (Nested Set).
Корневой элемент получил ключи 1 и 14, которые включают в себя диапазон чисел всех остальных ключей. Ветка VEGETABLE получила ключи 2 и 7, которые, в свою очередь, включают весь диапазон чисел ключей всех ее наследников и т.д. Вот они — вложенные множества. Все просто, не так ли?
Давайте воссоздадим такую же структуру в контексте таблицы БД.
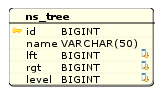
Рис. 6. Таблица иерархических данных на основе метода вложенных множеств
Или же в виде SQL:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | CREATE TABLE ns_tree ( `id` BIGINT NOT NULL AUTO_INCREMENT PRIMARY KEY, `name` VARCHAR(50) NOT NULL, `lft` BIGINT NOT NULL, `rgt` BIGINT NOT NULL, `level` BIGINT NOT NULL ) TYPE=InnoDB DEFAULT CHARSET=utf8; CREATE INDEX nslrl_idx ON ns_tree (lft, rgt, level); INSERT INTO ns_tree VALUES (1, 'FOOD', 1, 14, 0), (2, 'VEGETABLE', 2, 7, 1), (3, 'POTATO', 3, 4, 2), (4, 'TOMATO', 5, 6, 2), (5, 'FRUIT', 8, 13, 1), (6, 'APPLE', 9, 10, 2), (7, 'BANANA', 11, 12, 2); |
Как видите, мы ввели дополнительно еще одно поле в таблицу — level. В нем будет храниться информация об уровне вложенности каждой ветки дерева. В принципе, это делать вовсе не обязательно — уровень вложенности может быть достаточно просто вычислен, но так как данный алгоритм оптимизирован как раз для чтения, то почему бы не выиграть в производительности за счет кеширования информации об уровне? Риторический вопрос...
Чтение дерева из БД
Читаем все дерево:
1 2 3 4 5 6 | SELECT node.id, node.name, node.level FROM ns_tree AS node, ns_tree AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt AND parent.id = 1 ORDER BY node.lft; |
Результат будет таким:
+----+-----------+-------+ | id | name | level | +----+-----------+-------+ | 1 | FOOD | 0 | | 2 | VEGETABLE | 1 | | 3 | POTATO | 2 | | 4 | TOMATO | 2 | | 5 | FRUIT | 1 | | 6 | APPLE | 2 | | 7 | BANANA | 2 | +----+-----------+-------+
Теоретически, тот же результат мы бы могли получить, вычисляя уровень вложенности на лету:
1 2 3 4 5 6 | SELECT node.id, node.name, (COUNT(parent.id) - 1) AS level FROM ns_tree AS node, ns_tree AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt GROUP BY node.name ORDER BY node.lft; |
Попробуйте сравнить результат самостоятельно — он будет идентичен первому. Только сам запрос в данном случае более ресурсоемкий. А так как Nested Set — это оптимальный алгоритм чтения, то небольшая оптимизация в виде кеширования уровня вложенности рядом с остальными данными не такая уж и плохая стратегия.
Таким же, довольно несложным образом мы можем считывать целые ветки, пути из нашего дерева, обходить его узлы и т.д.
Например, если мы хотим извлечь все овощи (VEGETABLE) из нашего примера, это сделать достаточно просто:
1 2 3 4 | SELECT node.id, node.name, node.level FROM ns_tree AS node, ns_tree AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt AND parent.id = 2 ORDER BY node.lft; |
При этом, если необходимо исключить из результатов самого родителя вы можете поступить несколькими методами:
или другим способом — пусть это будет творческой задачей для читателя.
Да, быстрое и гибкое чтение, включая агрегацию с внешними связанными данными — конек данного алгоритма.
Тем не менее, не бывает худа без добра, и в данном случае, значительные трудности начинаются когда нам необходимо внести изменения в Nested Set дерево или удалить какую-либо из его ветвей.
Это связано, в первую очередь, с тем, что при изменениях, нам будет необходимо пересчитать все ключи той части дерева, которая находится справа от изменяемого узла, а также обновить информацию об уровнях вложенности. И все это не сделать одним простым запросом.
Смотрите сами.
Добавление новой ветки
Предположим, что мы хотим добавить новую ветку с именем SEA FOOD в наше дерево на одном уровне с VEGETABLES и FRUIT.
1 2 3 4 5 6 7 8 9 10 11 | BEGIN; SELECT @treeRight := rgt FROM ns_tree WHERE id = 2; /* справа от ветки VEGETABLES, у которой id = 2 */ UPDATE ns_tree SET rgt = rgt + 2 WHERE rgt > @treeRight; UPDATE ns_tree SET lft = lft + 2 WHERE lft > @treeRight; INSERT INTO ns_tree VALUES(0, 'SEA FOOD', @treeRight + 1, @treeRight + 2, 1); COMMIT; |
Если вы используете в MySQL таблицы MYISAM, или версию, которая не поддерживает транзакции, вы можете вместо BEGIN и COMMIT использовать блокировки на запись:
1 2 3 | LOCK TABLE ns_tree WRITE; ... UNLOCK TABLES; |
Как видите, задача на добавление новой ветки достаточно затратная и нетривиальная. Тем не менее, решаемая.
Удаление ветки
Давайте теперь попробуем удалить вновь созданную ветку:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | BEGIN; SELECT @treeLeft := lft, @treeRight := rgt, @treeWidth := rgt - lft + 1 FROM ns_tree WHERE id = 8; /* здесь идентификатор новой записи с именем 'SEA FOOD' */ DELETE FROM ns_tree WHERE lft BETWEEN @treeLeft AND @treeRight; /* ВНИМАНИЕ! Обратите внимание - мы не удаляем по id, Хотя в данном случае это бы нас устроило. Но в общем случае нам необходимо удалить всю ветку с ее содержимым! */ UPDATE ns_tree SET rgt = rgt - @treeWidth WHERE rgt > @treeRight; UPDATE ns_tree SET lft = lft - @treeWidth WHERE lft > @treeRight; COMMIT; |
Вывод — Nested Set действительно хорош, когда нам необходимо считывать структуру деревьев из БД. При этом он одинаково хорош для деревьев любого объема.
Тем не менее, для иерархических структур, которые подвергаются частому изменению он, очевидно, не будет являться оптимальным выбором.
А вот этот метод имеет отражение в Doctrine в виде реализации шаблона поведения, который мы можем привязать к нашей модели.
Сделать это довольно просто, методом конфигурации модели через YAML-конфиг или прамо в коде базового класса.
YAML:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | NsTree: tableName: ns_tree actAs: [NestedSet] columns: id: type: integer(8) primary: true autoincrement: true name: type: string(50) notnull: true lft: type: integer(8) notnull: true rgt: type: integer(8) notnull: true level: type: integer(8) notnull: true |
Как видите, достаточно просто указать actAs: [NestedSet] в описании класса.
Однако Doctrine предоставляет более гибкую конфигурацию NestedSet модели. Например, вы можете хранить в одной таблице несколько деревьев. Для этого, вам необходимо ввести в таблицу дополнительное поле, в котором вы будете хранить идентификатор корня дерева для каждой записи.
В этом случае конфигурацию следовало бы записать так:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | NsTree:
tableName: ns_tree
actAs:
NestedSet:
hasManyRoots: true
rootColumnName: root_id
columns:
id:
type: integer(8)
primary: true
autoincrement: true
root_id:
type: integer(8)
notnull: true
name:
type: string(50)
notnull: true
lft:
type: integer(8)
notnull: true
rgt:
type: integer(8)
notnull: true
level:
type: integer(8)
notnull: true |
Все то же самое могло бы быть проделано в существующем базовом классе модели.
Для первого случая:
1 2 3 4 5 6 7 8 | ... public function setTableDefinition() { ... $this->actAs('NestedSet'); ... } ... |
или:
1 2 3 4 5 6 7 8 | ... public function setTableDefinition() { ... $this->actAs('Doctrine_Template_NestedSet'); ... } ... |
Для второго случая (несколько деревьев):
1 2 3 4 5 6 7 8 9 10 | ... public function setTableDefinition() { ... $options = array('hasManyRoots' => true, 'rootColumnName' => 'root_id'); $this->actAs('NestedSet', $options); ... } ... |
Заметьте, Doctrine использует 'root_id' в качестве имени поля по умолчанию. Поэтому вам не обязательно указывать эту опцию, если оно совпадает с именем в вашей реальной таблице. В противном случае вы можете его задать.
Примеры работы с деревьями Nested Set в Doctrine
Извлекаем и печатаем все дерево на экран:
1 2 3 4 5 | $tree = Doctrine::getTable( 'NsTree')->getTree()->fetchTree(); echo "<pre>"; foreach ($tree as $node) { echo str_repeat( "\t", $node['level']) . $node['name'] . "\n"; } |
Посмотрите как это просто!
За дополнительными примерами и информацией вы можете обратиться к официальной документации Doctrine, разделы 8.2.4 и 8.2.5
Еще один довольно интересный подход для хранения иерархических структур. Основная идея алгоритма в хранении полного пути к узлу от вершины дерева. Выглядит это примерно так:

Рис. 7. Древовидная структура, организованная по принципу материализованый путь
Принцип формирования таких путей достаточно прост. Глубина пути — это уровень дерева. Внутри ветки нумерация — инкрементная. Другими словами, VEGETABLE — первый ребенок FOOD, FRUIT — второй ребенок и т.д.
Проще будет взглянуть на это в виде таблицы:
+---------------+-------+ | name | path | +---------------+-------+ | FOOD | 1 | | VEGETABLE | 1.1 | | POTATO | 1.1.1 | | TOMATO | 1.1.2 | | FRUIT | 1.2 | | APPLE | 1.2.1 | | BANANA | 1.2.2 | +---------------+-------+
Возможно, так даже более наглядно.
В базе данных все это находит следующее отражение.

Рис. 8. структура таблицы иерархических данных, организованных по принципу материализованный путь
Или в виде SQL:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | CREATE TABLE mp_tree ( `id` BIGINT NOT NULL AUTO_INCREMENT PRIMARY KEY, `name` VARCHAR(50) NOT NULL, `path` VARCHAR(100) NOT NULL ) TYPE=InnoDB DEFAULT CHARSET=utf8; CREATE INDEX mpp_idx ON mp_tree (`path`); INSERT INTO mp_tree VALUES (1, 'FOOD', '1'), (2, 'VEGETABLE', '1.1'), (3, 'POTATO', '1.1.1'), (4, 'TOMATO', '1.1.2'), (5, 'FRUIT', '1.2'), (6, 'APPLE', '1.2.1'), (7, 'BANANA', '1.2.2'); |
В чем же преимущество такого подхода?
Во-первых, по сравнению с Nested Set, он более поддается изменениям. В то же время остается достаточно удобным для выборки деревьев целиком и их частей. Но, и он не идеален. Особенно по части поиска предков ветки.
Поиск пути к узлу:
1 2 3 | SELECT t1.name from mp_tree t1, mp_tree t2 WHERE t2.path like CONCAT( t1.path, '.%') AND t2.id = 3; /* Поиск пути к узлу с именем 'POTATO' */ |
Результат:
+-----------+ | name | +-----------+ | FOOD | | VEGETABLE | +-----------+
Вычисление уровня вложенности.
Для решения этой задачи нам в принципе достаточно посчитать кол-во точек (или других разделителей, если вы используете не точку) в путях. К сожалению, MySQL не имеет подходящей функции, но мы можем ее реализовать достаточно просто своими силами:
1 2 3 4 5 6 7 8 9 10 11 12 13 | CREATE FUNCTION STRFIND (str VARCHAR(255), delimtr CHAR(1)) RETURNS INT BEGIN DECLARE _cnt INT; DECLARE _start INT; SET _cnt = -1; SET _start = 1; WHILE _start > 0 DO SET _start = LOCATE( delimtr, str); SET str = SUBSTRING( str, _start + 1); SET _cnt = _cnt + 1; END WHILE; RETURN _cnt; END |
Выбор ветки:
1 2 3 | SELECT name, strfind( path, '.') AS level FROM mp_tree WHERE path LIKE '1.1%'; /* Выбираем всю ветку 'VEGETABLES' */; |
Результат:
+-----------+-------+ | name | level | +-----------+-------+ | VEGETABLE | 1 | | POTATO | 2 | | TOMATO | 2 | +-----------+-------+
Обратите внимание, в данном примере мы воспользовались нашей самописной функцией и это было достаточно удобно.
Поиск родителя:
1 | SELECT t2.* FROM mp_tree t1, mp_tree t2 WHERE t1.id=3 AND t2.path=SUBSTRING( t1.path, 1, (LENGTH(t1.path) - LOCATE('.', REVERSE(t1.path)))); |
Как видите, все эти запросы не тешат максимальной производительностью (по сравнению с предыдущим методом), но, тем не менее, использование именно этого алгоритма может быть заметно удобнее, для деревьев, над которыми часто выполняются как операции чтения, так и изменения.
Насколько известно автору, алгоритм довольно уверенно себя чувствует на достаточно больших объемах данных.
Следует отметить, что наиболее неприятной в данном алгоритме будет операция вставки узла в середину уже существующей структуры (между другими узлами), т.к. это повлечет изменение всех путей в нижележащих узлах. Хотя, справедливости ради, следует сказать, что такая операция окажется нетривиальной для любой модели хранения данных. Другая тяжелая операция — это перенос одной ветки в другую.
А вот удаление, добавление в конец или изменение узла — это операции довольно простые, и, как правило, не вызывают сложностей в данной модели.
Как видно из примеров, данный алгоритм также можно несколько оптимизировать на чтение, путем введения ещё одного поля level, как это было сделано для списков смежных вершин (Nested Set). Однако это несколько усложнит операции добавления, изменения и удаления узлов дерева, т.к. уровни придется пересчитывать для всего или части дерева при каждом изменении. В конечном счете, именно разработчику решать, в какую сторону следует делать перекос производительности.
К сожалению, на данный момент, этот метод хранения деревьев пока не нашел своей реализации в ORM Doctrine (текущая версия на момент написания материала — 1.0.4, 1.1.0 — в альфа версии также реализации не имеет).
Тем не менее есть все предпосылки полагать, что его реализация появится в будущем, т.к. исходные коды библиотеки содержат в пакете Doctrine/Tree абстракный пустой класс с именем MaterializedPath.
Автор будет следить за событиями и обновит эту статью, как только реализация найдет свое отражение, так что можете сюда вернуться позже.
По сути вопроса следует отметить, что скомбинировать приведенные методы можно лишь в двух направлениях:
Комбинировать же Nested Set и Materialized Path особого смысла не имеет, т.к. существенного выигрыша ни в чтении, ни в записи вы не получите.
Фактически, комбинирование подходов на уровне БД ограничивается вводом поля, хранящего ссылку на родительскую запись в таблицы списков смежности и материализованных путей:
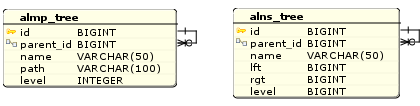
Рис. 9. Таблицы моделей иерархических структур данных AL+MP и AL+NS
Последствия такого подхода очевидны.
AL+MP
Для AL при использовании с MP:
Для MP при использовании с AL:
AL+NS
Для связки AL+NS взаимовыгодность не столь очевидна. В первую очередь это объясняется тем, что недостатки от проблем изменения узлов дерева в модели NS напрочь убивают в этой сфере все достоинства AL. Это значит, что такую связку следует рассматривать лишь как качественное улучшение поиска родителей и наследников заданного узла в алгоритме NS, а также как повышение надежности самого алгоритма (ключи можно всегда перестроить в случае порчи — информацию о связях хранит AL). Утверждение о повышении надежности справедливо и для предыдущей комбинации методов. Но ведь и это качественное улучшение, хотя и не такое очевидное, не так ли?
В данной статье мы рассмотрели несколько основных методов хранения иерархических данных в реляционных БД и очертили все их достоинства и недостатки. Также мы показали на практике, какие из них доступны для использования в реализации ORM Doctrine, и как их использовать.
Очевидно, что даже выбор того или иного метода в каждом конкретном случае — задача не такая уж и простая, но автор надеется, что данный материал будет способствовать принятию осознанного и правильного решения, а также будет способствовать творческому процессу поиска новых и более оптимальных решений.
Удачи в девелопменте!
В данной статье я постараюсь приоткрыть завесу над этим животрепещущим вопросом, а в следующей обещаю коснуться вопросов оптимизации и поисков нестандартных решений.
Итак, тестирование. Как и любое другое тестирование, наше также требует определенных действий по подготовке, анализу, выработке целей и плана действий.
Фактически, целью является проведение серии стресс-тестов различных алгоритмов на различных объемах данных. Неплохо было бы также прогнать тесты на нескольких различных аппаратных платформах, но, увы, автору это не по силам (время и деньги — всему виной).
Естественно, хорошо было бы провести тесты наиболее важных и значимых операций, которые как правило выполняются над теми или иными деревьями. После достаточно продолжительных размышлений было решено остановиться на таком списке тестируемых операций:
Стоит отметить, что данные операции мы приближаем к боевым условиям, т.е. входными данными для нас будут идентификаторы узлов и их родителей. Это позволит не привязываться к конкретным реализациям каждого из алгоритмов.
Далее оговорим, что нас интересует производительность чистого SQL, поэтому мы будем делать замеры исключительно его работы.
Автор не претендует на полноту заявленного списка операций. Возможно, кто-то вспомнит об операциях поиска соседей узла или выборке всех листов дерева, да еще и в заданной ветке — пожалуйста, каждый вправе расширить и дополнить данный эксперимент. Я же пока остановлюсь на приведенной, по моему мнению, основной минимальной функциональности.
Теперь я хочу остановиться несколько подробней на реализации самих функций, тесты над которыми в дальнейшем будут проведены. Но, если вам интересны лишь голые цифры и факты, — вы можете перейти к следующему разделу статьи.
Далеко не все заявленные функции имеют тривиальные решения в разных методах, тем более на чистом SQL. Например, выбор ветки в AL-дереве — задача сугубо рекурсивная. Но стоит ли этим заниматься на уровне SQL?...
В целом, следует учесть несколько следующих положений: — СУБД, на которой производятся тесты — MySQL версии 5.0.x. Движок — InnoDB (удобен для реализации каскадных операций для AL-Tree на уровне БД). — Запросы на выборку выполняются с флагом SQL_NO_CACHE, чтобы оценить «чистые» затраты на выполнение запросов. — Деревья различных типов имеют одинаковую физическую структуру узлов (т.е. случайным образом создается дерево одного типа, а остальные деревья строятся от первого). — Алгоритмы Nested Set и Materialized Path были усилены полем level, хранящем уровень вложенности текущего узла в дереве. В частности, можно говорить о том, что это позволяет увеличить, например, производительность выборки наследников узла в MP-дереве более чем в 100 раз! Фактически, без данного поля данные алгоритмы, в некотором смысле, теряют свою привлекательность. Поэтому, можно говорить не столько об их тюнинге при добавлении данного поля, сколько о необходимом условии их функционирования. Таким образом, структура нашей тестовой базы такова:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | -- Adjacency List Tree Structure CREATE TABLE `al_tree` ( `id` bigint(20) NOT NULL auto_increment, `parent_id` bigint(20) default NULL, `name` varchar(50) NOT NULL, PRIMARY KEY (`id`), KEY `fk_tree_tree` (`parent_id`), CONSTRAINT `fk_tree_tree` FOREIGN KEY (`parent_id`) REFERENCES `al_tree` (`id`) ON DELETE CASCADE ON UPDATE CASCADE ) ENGINE=InnoDB DEFAULT CHARSET=utf8 -- Nested Set Tree Structure CREATE TABLE `ns_tree` ( `id` bigint(20) NOT NULL auto_increment, `name` varchar(50) NOT NULL, `lft` bigint(20) NOT NULL, `rgt` bigint(20) NOT NULL, `level` bigint(20) NOT NULL, PRIMARY KEY (`id`), KEY `nslrl_idx` (`lft`,`rgt`,`level`) ) ENGINE=InnoDB DEFAULT CHARSET=utf8 -- Materialized Path Tree Structure CREATE TABLE `mp_tree` ( `id` bigint(20) NOT NULL auto_increment, `name` varchar(50) NOT NULL, `path` varchar(100) NOT NULL, `level` int(11) NOT NULL, PRIMARY KEY (`id`), KEY `mpp_idx` (`path`) ) ENGINE=InnoDB DEFAULT CHARSET=utf8 |
— Для работы с деревьями Nested Set и Materialized Path были написаны функции и процедуры на уровне базы данных для упрощения рутинных операций работы с деревьями. В частности, добавлены функции STRFIND, REPLACE_PATH и процедуры MOVE_NODE_NS, MOVE_NODE_MP, REMOVE_NODE_MP:
STRFIND( str, delimtr)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | -- -- Функция ищет количество вхождений символа delimtr в строку str. -- Фактически эта функция используется для поиска уровня -- вложенности узла в дереве типа MATERIALIZED PATH. -- (Кол-во разделителей в пути узла и есть уровень вложенности) -- -- @param str VARCHAR(255) - исходная строка -- @param delimtr CHAR(1) - искомый символ -- @return INT - кол-во вхождений -- CREATE FUNCTION `STRFIND`(str VARCHAR(255), delimtr CHAR(1)) RETURNS INT BEGIN DECLARE _cnt INT; DECLARE _start INT; SET _cnt = -1; SET _start = 1; WHILE _start > 0 DO SET _start = LOCATE( delimtr, str); SET str = SUBSTRING( str, _start + 1); SET _cnt = _cnt + 1; END WHILE; RETURN _cnt; END |
REPLACE_PATH( _str, _match, _replace)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | -- -- Функция замещает в заданной строке _str -- подстроку _match на строку _replace,. -- если _match найдена начиная от начала строки _str -- Удобна для использования в деревьях типа -- MATERIALIZED PATH для изменения путей. -- -- @param _str VARCHAR(255) - исходная строка -- @param _match VARCHAR(255) - подстрока поиска -- @param _replace VARCHAR(255) - подстрока замены -- @return VARCHAR(255) - новыя строка -- CREATE FUNCTION `REPLACE_PATH`( _str VARCHAR(255), _match VARCHAR(255), _replace VARCHAR(255)) RETURNS VARCHAR(255) BEGIN IF _str LIKE CONCAT(_match, '%') THEN RETURN CONCAT( _replace, SUBSTRING( _str, LENGTH(_match)+1, LENGTH(_str))); END IF; RETURN _str; END |
Главное отличие приведенной функции от встроенной REPLACE в том, что она гарантированно изменить заданную строку только если совпадение найдено С НАЧАЛА строки и внесет изменения лишь один раз.
MOVE_NODE_NS( node_id, parent_id)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 | -- -- ПРОЦЕДУРА ПЕРЕМЕЩЕНИЯ ВЕТКИ В ДЕРЕВЕ ТИПА NESTED SET -- -- @param node_id - идентификатор узла, который следует переместить -- @param parent_id - идентификатор узла в который следует переместить -- CREATE PROCEDURE MOVE_NODE_NS( node_id BIGINT, parent_id BIGINT) BEGIN DECLARE done INT DEFAULT 0; DECLARE c_id, c_lft, c_rgt, c_lvl, nWidth, nLeft, nRight, dtKey, nLvl, pRight, addLvl, addKey BIGINT; DECLARE c_name VARCHAR(50); -- Создаем курсор который будет хранить всю ветку, -- которую мы перемещаем DECLARE mvBranch CURSOR FOR SELECT id, name, lft - dtKey, rgt - dtKey, level - nLvl FROM ns_tree WHERE lft >= nLeft AND rgt <= nRight; DECLARE CONTINUE HANDLER FOR NOT FOUND SET done = 1; -- Собираем необходимые данные о выбранной ветке SELECT rgt - lft + 1, lft, rgt, lft - 1, level INTO nWidth, nLeft, nRight, dtKey, nLvl FROM ns_tree WHERE id = node_id; -- Выбираем ветку в курсор OPEN mvBranch; -- Удаляем ветку из дерева DELETE FROM ns_tree WHERE lft BETWEEN nLeft AND nRight; -- Обновляем ключи в дереве UPDATE ns_tree SET rgt = rgt - nWidth WHERE rgt > nRight; UPDATE ns_tree SET lft = lft - nWidth WHERE lft > nRight; -- выбираем данные о родителе в новом дереве SELECT rgt, level + 1 INTO pRight, addLvl FROM ns_tree WHERE id = parent_id; SELECT MAX(node.rgt) INTO addKey FROM ns_tree node, ns_tree parent WHERE node.lft BETWEEN parent.lft AND parent.rgt AND node.level = parent.level + 1 AND parent.id = parent_id; -- создаем в дереве пространство, куда будет -- помещена выбранная ранее ветка UPDATE ns_tree SET rgt = rgt + nWidth WHERE rgt >= pRight; UPDATE ns_tree SET lft = lft + nWidth WHERE lft > pRight; -- преобразуем ветку должным образом и вставляем. -- в новое дерево REPEAT FETCH mvBranch INTO c_id, c_name, c_lft, c_rgt, c_lvl; IF NOT done THEN INSERT INTO ns_tree VALUES (c_id, c_name, c_lft + addKey, c_rgt + addKey, c_lvl + addLvl); END IF; UNTIL done END REPEAT; CLOSE mvBranch; END |
MOVE_NODE_MP( node_id, parent_id)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 | -- -- ПРОЦЕДУРА ПЕРЕМЕЩЕНИЯ ВЕТКИ В ДЕРЕВЕ ТИПА MATERIALIZED PATH -- -- @param node_id - идентификатор узла, который следует переместить -- @param parent_id - идентификатор узла в который следует переместить -- CREATE PROCEDURE MOVE_NODE_MP( node_id BIGINT, parent_id BIGINT) BEGIN DECLARE done, m_cnt, m_rows, p_cnt, p_rows INT DEFAULT 0; DECLARE c_id, p_id, n_pos, n_lvl, np_id, np_lvl, new_pos, dt_lvl, ch_id, ch_pos BIGINT; DECLARE c_path, p_path, n_path, np_path, ch_path, new_path VARCHAR(100); -- Создаем курсор, в который выбираем ветку, -- которую следует переместить DECLARE mvBranch CURSOR FOR SELECT SQL_CALC_FOUND_ROWS node.id, node.path FROM mp_tree node, mp_tree parent WHERE node.path LIKE CONCAT(parent.path, '%') AND parent.id = node_id; -- Создаем курсор, в который вибираем все ветки справа -- от перемещаемой, находящиеся с ней на одном уровне DECLARE pChildren CURSOR FOR SELECT SQL_CALC_FOUND_ROWS node.id, node.path, CAST(SUBSTRING(REVERSE(node.path), 1, LOCATE('.', node.path)-1) AS UNSIGNED) as pos FROM mp_tree node, mp_tree parent WHERE node.path LIKE CONCAT(parent.path, '%') AND node.level = parent.level + 1 AND CAST(SUBSTRING(REVERSE(node.path), 1, LOCATE('.', node.path)-1) AS UNSIGNED) > n_pos AND parent.id = p_id ORDER BY pos; DECLARE CONTINUE HANDLER FOR NOT FOUND SET done = 1; -- Собираем необходимые данные SELECT path, CAST(SUBSTRING(REVERSE(path), 1, LOCATE('.', path)-1) AS UNSIGNED), level INTO n_path, n_pos, n_lvl FROM mp_tree WHERE id = node_id; SELECT parent.id, parent.path INTO p_id, p_path FROM mp_tree node, mp_tree parent WHERE parent.path = SUBSTRING( node.path, 1, (LENGTH(node.path) - LOCATE('.', REVERSE(node.path)))) AND node.id = node_id; SELECT id, path, level INTO np_id, np_path, np_lvl FROM mp_tree WHERE id = parent_id; -- Находим разницу в уровнях между уровнями перемещаемых узлов -- и новым родителем: SET dt_lvl = np_lvl - n_lvl + 1; SELECT MAX(CAST(SUBSTRING(REVERSE(node.path), 1, LOCATE('.', node.path)-1) AS UNSIGNED)) + 1 INTO new_pos FROM mp_tree node, mp_tree parent WHERE node.path LIKE CONCAT(parent.path, '%') AND node.level = parent.level + 1 AND parent.id = parent_id; -- Перемещаем ветку OPEN mvBranch; SELECT FOUND_ROWS() INTO m_rows; WHILE m_cnt < m_rows DO FETCH mvBranch INTO c_id, c_path; UPDATE mp_tree SET path = REPLACE_PATH(path, n_path, CONCAT(np_path, '.', new_pos)), level = level + dt_lvl WHERE id = c_id; SET m_cnt = m_cnt + 1; END WHILE; CLOSE mvBranch; -- Исправляем данные о путях в ветке из которой. -- переместили заданную ветку OPEN pChildren; SELECT FOUND_ROWS() INTO p_rows; WHILE p_cnt < p_rows DO FETCH pChildren INTO ch_id, ch_path, ch_pos; UPDATE mp_tree SET path = REPLACE_PATH(path, ch_path, CONCAT(p_path, '.', ch_pos - 1)) WHERE path LIKE CONCAT( ch_path, '%'); SET p_cnt = p_cnt + 1; END WHILE; CLOSE pChildren; END |
REMOVE_NODE_MP( node_id)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 | -- -- ПРОЦЕДУРА УДАЛЕНИЯ ВЕТКИ В ДЕРЕВЕ ТИПА MATERIALIZED PATH -- -- @param node_id - идентификатор узла, который следует удалить -- CREATE PROCEDURE REMOVE_NODE_MP( node_id BIGINT) BEGIN DECLARE n_pos, ch_id, p_id, ch_pos BIGINT; DECLARE n_path, ch_path, p_path VARCHAR(100); DECLARE done, p_cnt, p_rows INT DEFAULT 0; -- Создаем курсор, в который вибираем все ветки справа -- от перемещаемой, находящиеся с ней на одном уровне DECLARE pChildren CURSOR FOR SELECT SQL_CALC_FOUND_ROWS node.id, node.path, CAST(SUBSTRING(REVERSE(node.path), 1, LOCATE('.', node.path)-1) AS UNSIGNED) as pos FROM mp_tree node, mp_tree parent WHERE node.path LIKE CONCAT(parent.path, '%') AND node.level = parent.level + 1 AND CAST(SUBSTRING(REVERSE(node.path), 1, LOCATE('.', node.path)-1) AS UNSIGNED) > n_pos AND parent.id = p_id ORDER BY pos; DECLARE CONTINUE HANDLER FOR NOT FOUND SET done = 1; -- Собираем необходимые данные SELECT path, CAST(SUBSTRING(REVERSE(path), 1, LOCATE('.', path)-1) AS UNSIGNED) INTO n_path, n_pos FROM mp_tree WHERE id = node_id; SELECT parent.id, parent.path INTO p_id, p_path FROM mp_tree node, mp_tree parent WHERE parent.path = SUBSTRING( node.path, 1, (LENGTH(node.path) - LOCATE('.', REVERSE(node.path)))) AND node.id = node_id; -- Удаляем вветку DELETE FROM mp_tree WHERE path LIKE CONCAT( n_path, '%'); -- Исправляем данные о путях в ветке из удалили заданную ветку OPEN pChildren; SELECT FOUND_ROWS() INTO p_rows; WHILE p_cnt < p_rows DO FETCH pChildren INTO ch_id, ch_path, ch_pos; UPDATE mp_tree SET path = REPLACE_PATH(path, ch_path, CONCAT(p_path, '.', ch_pos - 1)) WHERE path LIKE CONCAT( ch_path, '%'); SET p_cnt = p_cnt + 1; END WHILE; CLOSE pChildren; END |
Фактически, теперь все тонкости реализации раскрыты, на этом можно остановиться и переходить к вопросам проведения тестов.
Тестирование производилось с помощью самописной консольной программы на следующей конфигурации:
Аппаратное обеспечение:
CPU: Intel® Core™2 Duo CPU E7200 @ 2.53GHz 6Mb 64bit
RAM: 4 Gb
HD: 2 x 250Gb 7200rpm RAID 1
Программное обеспечение:
OS: Debian Linux 2.6.26−1-amd64 (64bit)
PHP-CLI: 5.2.6−5 with Suhosin-Patch 0.9.6.2
MySQL: 5.0.51a, for debian-linux-gnu (x86_64) using readline 5.2
Скажем так, данный аппарат — это сервер, далеко не сильно загруженный на данный момент (около 100 000 достаточно простых HTTP-запросов в сутки), что для такой конфигурации практически не заметно.
Саму же программу вы можете скачать отсюда и попробовать произвести тестирование на своей машине (работает только в Unix-подобной среде). Инструкцию по работе с программой вы найдете в скачанном дистрибутиве в файле README.TXT.
Во время проведения тестирования было выбрано 5 конфигураций деревьев:
Это деревья, тесты над которыми удалось успешно завершить. Все тесты были завершены чуть меньше чем за 6 часов, при этом основное время, естественно, занял последний тест с деревьями в полмиллиона узлов.
Алгоритм создания деревьев работает таким образом, что закон распределения узлов по дереву примерно следующий:
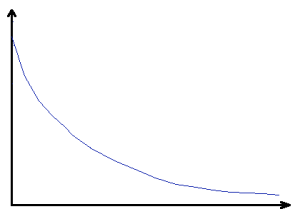
Где по оси абсцисс — идентификаторы узлов по возрастанию, а по оси ординат — количество узлов в ветках узла с заданным идентификатором.
В связи с таким положением вещей была выбрана следующая схема тестированя. На выборку — итеративная пошаговая схема для проверки функционирования алгоритмов выборки на разных участках дерева. Итерации организованы следующим способом:
id > 1 < 10 - шаг 1 id > 10 < 100 - шаг 10 id > 100 < 1000 - шаг 100 id > 1000 < 10000 - шаг 1000 id > 10000 < 100000 - шаг 10000 id > 100000 - шаг 100000
Это позволяет отследить зависимость функций поиска и выборки от закона распределения узлов.
Для функций изменения схема выбрана несколько иная. Поскольку сами операции изменения для большинства алгоритмов — это достаточно затратные операции, проверять их итеративным способом нет смысла (слишком сильно увеличивается время ожидания завершения тестирования). Поэтому, способ проверки основан на проведении изменений в одном из наибольших узлов, который расположен в начале дерева. К тому же, такой тест будет выполнен единожды. Для того, чтобы обрисовать общую картину и обозначить круг проблем — этого вполне достаточно.
Итак, тесты выполнены, данные собраны. Я считаю, что нет смысла вываливать в данной статье все те цифры, которые мы получили в результатах. Тем не менее они доступны для скачивания в виде архива. Так что все желающие могут на них посмотреть воочию.
Куда же более интересным будет показать эмпирически, каковы данные результаты. Давайте посмотрим на что похожи некоторые графики для дерева в 100 000 узлов.
Все ниже посчитано и указанно в секундах.

Рис. 1. Выборка всего дерева целиком
На последующих графиках отображена зависимость флуктуаций функций выборки от поиска на разных участках дерева. Фактически цифрами по оси ординат отмечены шаги, о которых речь шла выше.
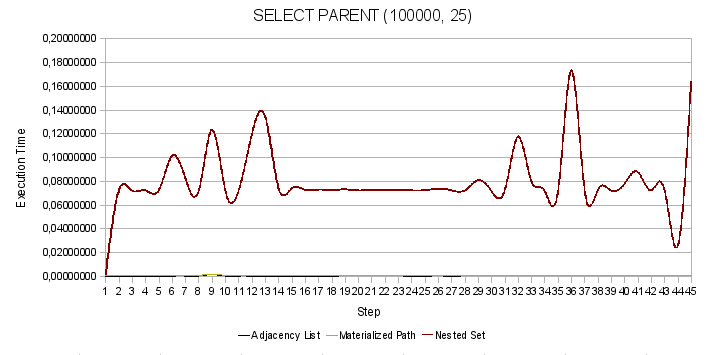
Рис. 2. Поиск узла-родителя
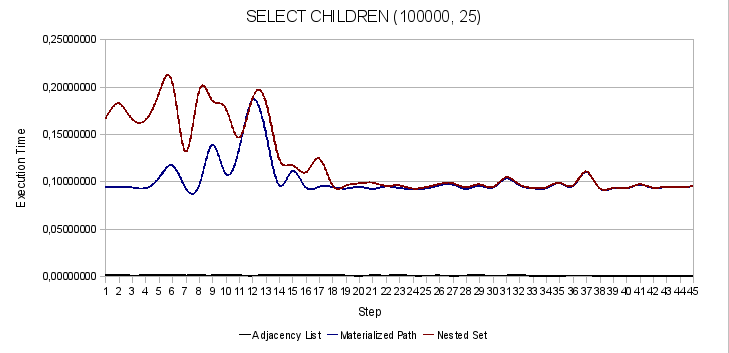
Рис. 3. Поиск наследников заданного узла
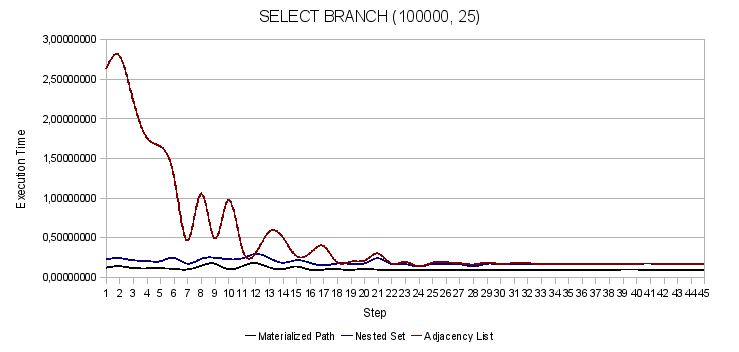
Рис. 4. Выбор всей ветки заданного узла
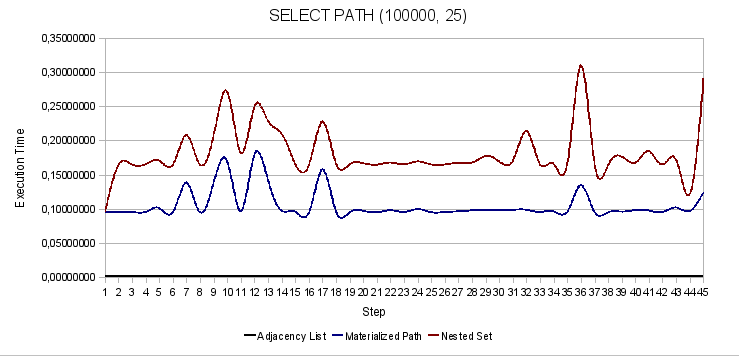
Рис. 5. Поиск полного пути от корня к заданному узлу
Далее проиллюстрированы функции изменения, которые проводились над деревьями различных типов.
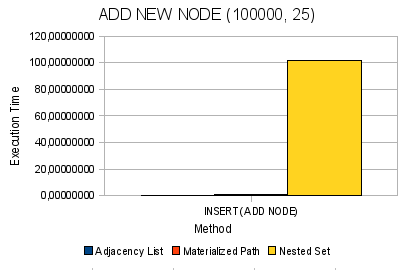
Рис. 6. Добавление нового узла в дерево
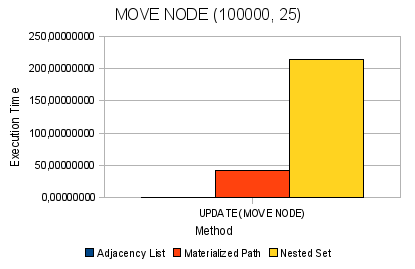
Рис. 7. Перемещение узла
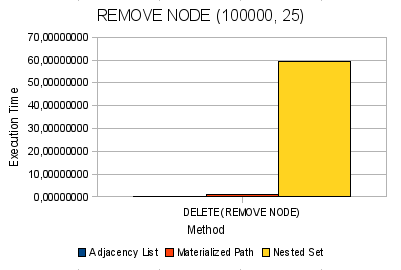
Рис. 8. Удаление узла и всех его потомков из дерева
Обобщенно же, в абсолютных цифрах можно сделать такие выводы:
Списки смежности (Adjacency List):
| Узлов | ALL | PATH | BRANCH | PARENT | CHILDREN | ADD | MOVE | REMOVE |
| 100 | 0,00245 | 0,00016 | 0,00416 | 0,00009 | 0,00011 | 0,00059 | 0,00037 | 0,00009 |
| 1000 | 0,00335 | 0,00025 | 0,03579 | 0,00009 | 0,00011 | 0,00387 | 0,00037 | 0,00009 |
| 10000 | 0,01244 | 0,00058 | 0,38146 | 0,00024 | 0,00036 | 0,03548 | 0,00081 | 0,00011 |
| 100000 | 0,10798 | 0,00105 | 2,55379 | 0,00155 | 0,00138 | 0,06382 | 0,00119 | 0,13931 |
| 500000 | 0,62305 | 0,00124 | 43,91373 | 0,00053 | 0,00209 | 0,05232 | 0,00077 | 0,00041 |
Вложенные множества (Nested Set)
| Узлов | ALL | PATH | BRANCH | PARENT | CHILDREN | ADD | MOVE | REMOVE |
| 100 | 0,00020 | 0,00015 | 0,00020 | 0,00017 | 0,00019 | 0,00367 | 0,02285 | 0,00314 |
| 1000 | 0,00129 | 0,00040 | 0,00093 | 0,00017 | 0,00059 | 0,02593 | 0,19237 | 0,02619 |
| 10000 | 0,01387 | 0,00433 | 0,00825 | 0,01771 | 0,00460 | 0,38235 | 1,37070 | 0,37219 |
| 100000 | 0,17165 | 0,07634 | 0,14261 | 0,17218 | 0,09953 | 101,749 | 213,461 | 59,1912 |
| 500000 | 0,83033 | 0,41670 | 0,62517 | 0,42942 | 0,15318 | 1427,96 | 3712,30 | 1627,97 |
Материализованный путь (Materialized Path)
| Узлов | ALL | PATH | BRANCH | PARENT | CHILDREN | ADD | MOVE | REMOVE |
| 100 | 0,00020 | 0,00017 | 0,00020 | 0,00016 | 0,00019 | 0,00076 | 0,02633 | 0,00059 |
| 1000 | 0,00137 | 0,00069 | 0,00107 | 0,00016 | 0,00071 | 0,00136 | 0,22232 | 0,00136 |
| 10000 | 0,01560 | 0,00608 | 0,01372 | 0,00056 | 0,00737 | 0,00679 | 1,44434 | 0,00801 |
| 100000 | 0,18680 | 0,10466 | 0,17608 | 0,00064 | 0,18546 | 0,92136 | 41,5875 | 1,06560 |
| 500000 | 0,99102 | 0,56412 | 0,59418 | 0,00090 | 0,56800 | 2,02149 | 2950,40 | 1,67124 |
Давайте подумаем, о чем говорят все эти цифры и графики.
Во-первых, все алгоритмы на малых объемах данных (до 10 000 узлов включительно) показали достаточно приемлемую производительность на всех функциях.
Во-вторых, проблемные операции существуют, а именно:
Выборка ветки целиком в дереве AL. Посмотрите, данная операция занимает до 2,5 секунд.
Хотелось бы отметить, что мы немного схитрили в нашем тесте. И вот каким образом. В алгоритме списков смежности (AL) мы реализовали выбор пути методом множественных JOIN'ов таблицы с собой же. Да, результат впечатляющий, особенно в сравнении с результатом выборки ветки рекурсивным способом. Но вряд ли вы выберите такой путь реализации данной функции для своего приложения. Разве что в качестве временной оптимизации. Ведь вам нужно знать максимальный уровень вложенности и не попасть под ограничение СУБД на количество JOIN'ов в одном запросе. Мы же просто провели тест.
Далее у нас возникают проблемы с операциями перемещения узла в алгоритмах NS и MP начиная от 10 000 узлов в дереве (свыше 1 секудны) и далее все становиться ещё хуже — на 100 000 узлах для MP — этот показатель свыше 40 секунд, для NS — почти 4 минуты. На 500 000 узлов цифры и вовсе переходят все рамки разумных пределов — почти 50 минут для MP и свыше 1 часа для NS.
Для NS похожая картина складывается и в остальных операциях изменения. На 10 000 элементов добавление занимает свыше 1,5 минут, а на 500 000 уже свыше 23 минут. С удалением та же проблема — почти минута для 100 000 узлов и свыше 27 минут на 500 000 узлов.
MP ж довольно уверенно себя чувствует и на достаточно больших объемах в операциях удаления и добавления узлов. На деревьях в 100 000 элементов эти операции протекают в пределах 1 секунды, что является более чем положительным результатом. И даже на 500 000 узлах эти операции происходят в пределеах нескольких секунд.
А это значит, что Nested Set следует использовать с фактически статичными деревьями, которые если и изменяются, то крайне редко. При этом, стоит и вовсе задуматься о создании инструмента, который перестраивает дерево по запросу полностью, используя в базовой основе AL-схему (как это делает наша программа генерации произвольных случайных деревьев). Это, как свидетельствуют факты гораздо быстрее, чем рутины самого NS. Либо вообще отказаться от данного алгоритма в пользу Materialized Path.
Как мы смогли выяснить, востребованность таких алгоритмов, как Nested Set и Materialized Path обусловлена, в первую очередь, большими объемами данных, где они могут оптимизировать некоторые запросы на поиск и выборку, которые будут критичными для приложения. Или же в условиях высоких нагрузок, где также важна оптимизация запросов. В данном случае речь идет об оптимизации таких операций, как поиск пути и выборка всей ветки в Adjacency List дереве. На практике также стоит говорить и об оптимизации операций поиска соседей, выбора «листьев» всего дерева или в ветке заданного узла, а также других не рассмотренных здесь операций (которые, по сути, для AL сложнореализуемы на уровне SQL-запросов).
На фоне полученных результатов Nested Set качественно уступает Materialized Path, который достаточно уверенно себя чувствует и в операциях на удаление и добавление (а как часто вы перемещаете узлы в ваших деревьях?...). Кроме того, я вижу неплохие перспективы оптимизации данного алгоритма, о чем мы поговорим в следующей статье.
Удачи в девелопменте!
|
Закладки на сайте Проследить за страницей |
Created 1996-2025 by Maxim Chirkov Добавить, Поддержать, Вебмастеру |