Previous: 2.9.1 Используемые стандарты    UP: 2.6 Методы сжатия информации
Down: 3 Каналы передачи данных
    Next: 3 Каналы передачи данных

Данная статья имеет целью познакомить с терминологией и математическими основами статистической теории передачи данных. Именно на этой математической основе зиждятся приведенные выше теоремы Шеннона и Найквиста. Статья является компиляцией из нескольких источников (Ю.В.Прохоров, Ю.А.Розанов "Теория вероятностей. Основные понятия, предельные теоремы, случайные процессы" Наука, М. 1967; Л.Ф. Куликовский, В.В.Мотов, "Теоретические основы информационных процессов", Высшая школа, 1987; Р. Галлагер "Теория информации и надежная связь" Советское радио, 1974 и др.). Материалы, предлагаемые здесь не могут считаться исчерпывающими и призваны быть поводом для более углубленного изучения по существующим монографиям.

Канал связи предназначен для транспортировки сообщений. Математическая модель канала связи описывается некоторой совокупностью Х ₁ элементов х₁ (X₁ = {x₁₁, x₁₂,, .x_1j }), называемых сигналами на входе канала, совокупностью Х₂ элементов х ₂ (x₂ = {x₂₁, x₂₂,, .x_2k}), называемых выходными сигналами, и условными распределениями вероятностей p₂=p₂(a₂ |x₁) в пространстве x₂ выходных сигналов x₂ . Если посланный сигнал (сигнал на входе) есть х₁ , то с вероятностью P₂=P₂(A₂|x₁ ) на выходе канала будет принят сигнал х₂ из некоторого множества A₂ М Х₂ (распределения задают вероятности того или иного искажения посланного сигнала х₁ ). Совокупность всех возможных сообщений обозначим символом x₀. Предполагается, что каждое из сообщений x₀ О X₀ может поступать с определенной вероятностью. То есть, в пространстве X₀ имеется определенное распределение вероятностей P₀=P₀(A₀ ).

Сообщения х₀ не могут быть переданы по каналу связи непосредственно, для их пересылки используются сигналы x₁ О X₁ . Кодирование сообщений х₀ в сигналы х₁ описывается при помощи условного распределения вероятностей P₁=P₁(A₁ |x₀). Если поступает сообщение х₀, то с вероятностью P₁=P₁(A₁|x₀) будет послан один из сигналов х₁ , входящих в множество A₁ М Х₁ (условные распределения P₁(A₁|x₀) учитывают возможные искажения при кодировании сообщений). Аналогичным образом описывается декодирование принимаемых сигналов х₂ в сообщения x₃ . Оно задается условным распределением вероятностей P₃=P₃(A₃|x₂) на пространстве Х₃ сообщений х₃ , принимаемых на выходе канала связи.

На вход канала связи поступает случайное сообщение x ₀ с заданным распределением вероятностей P₀=P₀(A₀ ). При его поступлении передается сигнал x ₁, распределение вероятностей которого задается правилом кодирования P₁=P₁(A₁|x₀):

P{x ₂ О A₂|x ₀, x ₁} = P₂(A₂|x ₁)

Принятый сигнал x ₂ декодируется, в результате чего получается сообщение x ₃:

P{x ₃ О A₃|x ₀, x ₁, x ₂} = P₃(A₃| x ₂)

Последовательность x ₀ ╝ x ₁ ╝ x ₂ ╝ x ₃ является марковской. При любых правилах кодирования и декодирования описанного типа имеет место неравенство:

I(x _0, x ₃) ё I(x _1, x ₂),

где I( x _0, x ₃) - количество информации о x ₀ в принятом сообщении x ₃, I(x _1, x ₂) - количество информации о x ₁ в принятом сигнале x ₂.

Предположим, что распределение вероятности входного сигнала x ₁ не может быть произвольным и ограничено определенными требованиями, например, оно должно принадлежать классу W. Величина C = sup I(( x ₁ , x ₂) , где верхняя грань берется по всем возможным распределениям P1 О W, называется емкостью канала и характеризует максимальное количество информации, которое может быть передано по данному каналу связи (теорема Шеннона).

Предположим далее, что передача сообщений x ₀ ╝ x ₃ должна удовлетворять определенным требованиям точности, например, совместное распределение вероятностей P _{x0 x1} передаваемого и принимаемого сообщений x ₀ и x ₃ должно принадлежать некоторому классу V. Величина H= inf I( x ₀ x ₃), где нижняя грань берется по всем возможным распределениям P _x0 x3 О V, характеризует минимальное количество информации, которое должно заключать в себе принимаемое сообщение x ₃ о x ₀, чтобы было выполнено условие точности передачи. Величина H называется энтропией источника сообщений.

Если возможна передача x ₀ ╝ x ₁ ╝ x ₂ ╝ x ₃ с соблюдением требований V и W, то есть существуют соответствующие способы кодирования и декодирования (существуют условные распределения P₁, P₂ и P₃), то H ё С.

Для выполнения этого неравенства передача является возможной, т.е. возможна передача последовательно поступающих сообщений

Предположим, что совокупность Х₀ всех возможных сообщений х₀ является дискретной (имеется не более чем счетное число различных сообщений x₀ , поступающих с соответствующими вероятностями P₀(x₀), x₀ О X₀ ) и условие точности передачи v состоит в том, что принимаемое сообщение x ₃ должно просто совпадать с переданным сообщением x ₃ = x ₀ с вероятностью 1. Тогда

Предположим далее, что имеется лишь конечное число N различных входных сигналов х₁ и нет никаких ограничений на вероятности P{ x ₁ = x₁}, x₁   О  X₁. Кроме того, предположим, что передаваемые сигналы принимаются без искажений, то есть с вероятностью 1 x ₂= x ₁ . Тогда емкость канала выражается формулой C = log ₂N, т.е. передаваемое количество информации I( x ₁, x ₂ ) будет максимальным в том случае, когда сигналы x₁ О X₁ равновероятны.

Если сообщения поступают независимо друг от друга, то количество информации, которое несет группа сообщений есть

группа сообщений, поступающая на кодирование с вероятностью

Пусть H<C, положим также d=(1/2)(C-H). Согласно закону больших чисел, примененному к последовательности независимых и одинаково распределенных случайных величин

с математическим ожиданием

для любого e >0 найдется такое n(e), что при всех n Ё n(e )

P{-H-d ё (1/n)logP( x _0n) ё H+d } Ё 1-e, где

Полученное неравенство говорит о том, что все группы сообщений х_0n можно разбить на два класса. К первому классу относятся высоковероятные сообщения х _0n, для которых P(x_0n) Ё 2^{-n(H+d )} и количество которых M_n не больше чем 2^{n(H+d )}:

Ко второму классу относятся все остальные маловероятные сообщения х_0n :
.

Каждую группу высоковероятных сообщений х_0n можно в принципе передать, закодировав ее соответствующей комбинацией сигналов . Число всевозможных комбинаций такого вида есть N_n=2^nC, и видно, что M_n<N_n. Имеется N_n различных сигналов x_1n, с помощью которых можно закодировать и передать безошибочно все M_n высоковероятных сообщений x_0n Если в дополнение к этому при поступлении любого маловероятного сообщения x_0n передавать некоторый один и тот же сигнал (отличный от сигналов, при помощи которых передаются высоковероятные сообщения x_0n , то с вероятностью, не меньшей чем 1-e, на выходе канала связи будет приниматься последовательность :

.

При выполнении неравенства H < C оказывается возможной передача достаточно длинных сообщений с той оговоркой, что с вероятностью e (e - наперед заданное сколь угодно малое положительное число) может быть допущена ошибка. Имеется целое семейство каналов связи и источников сообщений, зависящих от параметра n.

Количество информации I( x ₀, x ₃ ) для абстрактных случайных величин x ₀ и x ₃ со значениями в пространствах Х₀ и Х₃ может быть записано в виде:

I( x ₀, x ₃) = Mi(x ₀, x ₃), где

- информационная плотность. Последовательность пар ( x _0n, x _3n) называется информационно устойчивой, если при n ╝ ╔

I( x ₀, x ₃) ╝ ╔ и

(по вероятности)

Рассмотренная выше последовательность ( x _0n, x _3n), x _3n= x _0n поступающих сообщений x _0n =( ) обладает свойством информационной устойчивости, что в конечном счете и определило возможность передачи сообщений x _0n с точностью до e. Этот факт допускает широкое обобщение. Например, если С_n - пропускная способность канала
x _1n ╝ x _2n, H_n - минимальное количество информации, необходимое для соблюдения требуемой точности передачи x _0n ╝ x _3n, причем

(при n ╝ ╔ ),

и существуют информационно устойчивые последовательности пар ( x _0n, x _3n ) и ( x _1n, x₂n ), для которых одновременно

то при весьма широких предположениях для любого наперед заданного e >0 существует такое n(e), что по всем каналам связи с параметром n Ё n(e) возможна передача с точностью до e.

Как было указано выше, канал характеризуется условными распределениями З₂, задающими вероятности тех или иных искажений посылаемого сигнала х₁. Несколько изменим схему канала связи, считая, что имеется некоторое множество Z возможных состояний z канала связи, причем если канал находится в некотором состоянии z и на входе возникает сигнал x₁, то независимо от других предшествующих обстоятельств канал переходит в другое состояние z₁. Этот переход подвержен случайностям и описывается условными распределениями P(C|x₁, z) (P(C|x₁, z) - вероятность того, что новое состояние z₁ будет входить в множество C М Z). При этом уже считается, что выходной сигнал х₂ однозначно определяется состоянием канала z₁, т.е. существует некоторая функция j = j (z) на пространстве z возможных состояний канала такая, что х₂= j (z₁). Эта более общая схема позволяет учитывать те изменения, которые в принципе могут возникать в канале по мере его работы.

Рассмотрим стационарный режим работы канала связи. Предположим, что последовательно передаваемые сигналы
.., x ₁(-1), x ₁(0), x ₁(1),., соответствующие состояниям канала ., z (-1), z (0), z (1),., и определяемые ими сигналы
., x ₂(-1), x ₂(0), x ₂(1),., на выходе образуют стационарные и стационарно связанные случайные последовательности. Величина С=supI(x ₁,x ₂), где I(x ₁,x ₂), означает скорость передачи информации о стационарной последовательности {x ₁(n)} последовательностью {x ₂(n)} и верхняя грань берется по всем допустимым распределениям вероятностей входной последовательности {x ₁(n)}, называется пропускной способностью канала связи.

Предположим, что поступающие на вход канала связи сообщения {x ₀(n)}, n =., -1, 0, 1 ,., образуют случайную последовательность. Будем считать правило кодирования заданным, если при всех k, m и k ₁,., k_m Ё k определены условные вероятности

P{x ₁(k₁) О B₁,., x ₁ (k_m)О B_m|x ₀(-╔ ,k)}

Того, что при поступлении последовательности сообщений

x ₀(-╔ ,k) = ., x ₀(k-1), x ₀(k)

на соответствующих местах будут переданы сигналы x ₁(k₁),., x ₁(k_m), входящие в указанные множества B ₁, ., B_m. Эти вероятности считаются стационарными в том смысле, что они не меняются при одновременной замене индексов k и k₁,.,k_m на k+l и k₁+l,.,k_m+l при любом целом l. Аналогичными вероятностями p{ x ₃(k₁) О D₁,., x ₃(k_m) О D_m|x ₂(-╔ ,k)} задается правило декодирования.

Определим величину H формулой H = inf I( x ₀,x ₃), где I(x ₀, x ₃) - скорость передачи информации о стационарной последовательности {x ₀(n)} последовательностью {x ₃(n)}, n = ., -1, 0, 1,. (эти последовательности предполагаются стационарно связанными), и нижняя грань берется по всем допустимым распределениям вероятностей, удовлетворяющим требованиям точности передачи {x ₀(n)} ╝ { x ₃(n)}.

Неравенство H ё C является необходимым условием возможности передачи

{x ₀(n)} ╝ {x ₁(n)} ╝ {x ₂(n)} ╝ {x ₃(n)}.

Напомним, что каждое сообщение x ₀(n) представляет собой некоторый элемент х₀ из совокупности Х ₀ . Можно интерпретировать Х₀ как некоторый алфавит, состоящий из символов х₀ . Предположим, что этот алфавит Х₀ является конечным и требование точности передачи состоит в безошибочном воспроизведении передаваемых символов:

P{x ₃(k) = x ₃(k)} =1 для любого целого k.

Предположим также, что имеется лишь конечное число входных сигналов х₁ и состояний канала z. Обозначим состояния канала целыми числами 1, 2, ., N, и пусть p(k, x₁,j) - соответствующие вероятности перехода из состояния k в состояние j при входном сигнале x₁:

p(k,x₁,j) = P{z (x+1) = j|z (n)=k, x ₁(n+1)=x₁}.

Дополнительно предположим, что любые произведения вида

p(k₀,x₁(1),k₁)p(k₁,x₁(2),k₂). p(k_n-1,x₁(n),k_n)

являются стохастическими матрицами, задающими эргодические цепи Маркова. Это условие будет выполнено, если, например, каждая из переходных матриц {p(k,x₁,j)} имеет положительный коэффициент эргодичности. Тогда при выполнении неравенства H<C и соблюдении условия эргодичности стационарной последовательности {x ₀(n)} сообщений на входе передача возможна с точностью до любого e >0, т.е. при соответствующих способах кодирования и декодирования принимаемая последовательность сообщений {x ₃(n)} будет обладать тем свойством, что p{x ₃(k) N x ₀(k)} < e для любого целого k.

Пусть x ₁ = {x (t), t О T₁} и x ₂= {x (t), t О T₂} - два семейства случайных величин, имеющих совместное гауссово распределение вероятностей, и пусть H₁ и H ₂ - замкнутые линейные оболочки величин x (t), t О T₁, и x (t), t О T₂, в гильбертовом пространстве L² (W). Обозначим буквами P₁ и P₂ операторы проектирования на пространства H₁ и H₂ и положим P⁽¹⁾ = P₁P₂P₁, P⁽²⁾ = P₂P₁P₂. Количество информации I(x ₁,x ₂) о семействе величин x ₁, содержащееся в семействе x ₂, конечно тогда и только тогда, когда один из операторов P⁽¹⁾ или P⁽²⁾ представляет собой ядерный оператор, т.е. последовательность l ₁, l ₂,. его собственных значений (все они неотрицательны) удовлетворяет условию . При этом

.

В случае, когда x ₁ и x ₂ образованы конечным числом гауссовых величин:

x ₁={x (1),., x (m)}, x ₂ = {x (m+1),., x (m+n)}, причем корреляционная матрица B общей совокупности x (1),., x (m+n) является невырожденной, количество информации I(x ₁ , x ₂) может быть выражено следующей формулой:

,

где B₁ и B₂ - корреляционные матрицы соответствующих совокупностей x ₁ и x ₂ .

Гауссовы распределения обладают следующим экстремальным свойством. Для произвольных распределений вероятностей величин

x ₁ = {x (1), ., x (m)} и x ₂ = {x (m+1), ., x (m+n)}

с соответствующими корреляционными матрицами B₁, B₂ и B количество информации I(x ₁ , x ₂) удовлетворяет неравенству

Пусть x = (x ₁,.,x _n) и h = (h ₁,.,h _n) - векторные случайные величины в n-мерном евклидовом пространстве X и r(x,y) - некоторая неотрицательная функция, определяющая условие близости величин x и h, которое выражается следующим соотношением:

Mr(x ,h ) ё e .

Величину H=H _e , определенную как H _e = inf I(x, h), обычно называют e-энтропией случайной величины x (нижняя грань берется по всем случайным величинам h, удовлетворяющим указанному условию e-близости случайной величине x).

Пусть r(x,y) = r(|x-y|) и существует производная r'(0), 0< r'(0)<╔. Тогда при e ╝ 0 имеет место асимптотическая формула, в которой логарифмы берутся по основанию e:

где g() - гамма функция и h(x) - дифференциальная энтропия случайной величины x:

(p _x (x) - плотность распределения вероятностей, удовлетворяющая весьма широким условиям, которые выполняются, например, если плотность p _x (x) ограничена и h(x ) > -╔ ).
Пусть (a, b > 0)

Тогда

В частности, при a =2, b =1 имеет место асимптотическая формула

Пусть пара случайных процессов (x ₁(t), x ₂(t)) образует стационарный в узком смысле процесс, x ^[u,v] - совокупность значений x (t), u ё t ё v, и пусть
- условное количество информации о процессе x ₁= , содержащееся в отрезке процесса x ₂. Среднее количество указанной информации представляет собой линейно растущую функцию от t:

Фигурирующая здесь величина I(x₁ , x₂ ) называется средней скоростью передачи информации стационарным процессом x₂ о стационарном процессе x ₁ или просто - скоростью передачи информации.

Скорость передачи информации I(x ₁,x ₂) обладает рядом свойств, аналогичных свойствам количества информации. Но она имеет и специфические свойства. Так для всякого сингулярного случайного процесса x ₂ , т.е. такого процесса, все значения x ₂(t) которого являются функциями от совокупности величин (t₀ может быть выбрано любым), имеет место равенство I(x ₁, x ₂)=0.

Для всякого регулярного случайного процесса x ₂ равенство I(x ₁,x ₂)=0 справедливо лишь тогда, когда случайный процесс x ₁ не зависит от процесса x ₂ (это говорит о том, что в некоторых случаях I(x ₁,x ₂) N I(x ₂,x ₁) ).

При дополнительных условиях типа регулярности скорость передачи информации I(x ₁,x ₂) совпадает с пределом

,

где - количество информации об отрезке процесса , заключенное в . Так будет, например тогда, когда время меняется дискретно, а отдельные величины x ₁(t) и x ₂(t) могут принимать лишь конечное число различных значений или когда распределение вероятностей процессов x ₁ и x ₂ является гауссовым. В случае непрерывного времени t так будет для гауссовых процессов, когда спектральная плотность f(l) процесса x ₂(t) удовлетворяет условию

0< c ё l ²ⁿf(l ) ё c < ╔

Пусть стационарный процесс x = x (t) представляет собой последовательность величин, каждая из которых принимает значения из некоторого алфавита x, состоящего из конечного числа символов x₁, x₂,.,x_n. Предположим, что вероятность появления на фиксированном месте определенного символа x_i есть p_i, а вероятность появиться за ним символу x_j не зависит от предшествующих x_i значений и есть p_ij:

P{x (t) = x_i} = p_i, P{x(t+1) = x_i x_i|x(t) = x_i, x(t-1),., } = p_ij

Другими словами x = x (t) - стационарная цепь Маркова с переходными вероятностями {p _ij} и стационарным распределением {p _i}. Тогда скорость передачи информации стационарным процессом x(t) будет

I(x,x) = -

В частности, если x = x(t) - последовательность независимых величин (в случае p _ij = p_j), то

I(x,x) = -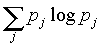

Пусть x ₁ = x ₁(t) и x ₂ = x ₂(t) - стационарные гауссовы процессы со спектральными плотностями f₁₁(l), f₂₂(l) и взаимной спектральной плотностью f₁₂(l) причем процесс x ₂ = x ₂(t) является регулярным. Тогда

I(x ₁, x ₂) = -

Рассмотрим следующее условие близости гауссовых стационарных процессов x ₁ (t) и x ₂(t):

M|x ₁(t) - x ₂(t)|² ё d ²

Наименьшая скорость передачи информации
H = inf I(x ₁,x ₂), совместимая с указанным условием "d-точности", выражается следующей формулой:

где

,

а параметр q ² определяется из равенства

.

Эта формула показывает, какого типа спектральная плотность f₂₂(l) должна быть у регулярного стационарного процесса x ₂(t), который несет минимальную информацию I (x ₁,x ₂) " H о процессе x ₁(t). В случае дискретного времени, когда f₁₁(l ) Ё q ² при всех l , -p ё l ё p, нижняя грань H скорости передачи достигается для такого процесса x ₂ (t) (со спектральной плотностью f₂₂(l), задаваемой приведенной выше формулой), который связан с процессом x ₁ (t) формулой
x ₂ (t) = x ₁ (t) + z(t), где z(t) - стационарный гауссов шум, не зависящий от процесса x ₂ (t); в общем случае формула f ₂₂(l) задает предельный вид соответствующей спектральной плотности регулярного процесса x ₂ (t).

В случае, когда спектральная плотность f ₁₁(l) приближенно выражается формулой

соответствующая минимальная скорость передачи информации H может быть вычислена по приближенной формуле , s ² = M[x(t)]².

2.10.3. Симметричный канал без памяти

Рассмотрим симметричный канал передачи данных без памяти c конечным числом входных сигналов х₁ , когда передаваемый сигнал х₁ с вероятностью 1-p правильно принимается на выходе канала связи, а с вероятностью p искажается, причем все возможные искажения равновероятны: вероятность того, что на выходе будет сигнал х₂ , равна для любого х₂ N x₁, где N - общее число сигналов. Для такого канала связи пропускная способность
c = sup I( x ₁,x ₂) достигается в случае, когда на вход поступает последовательность независимых и равномерно распределенных сигналов ., x ₁(-1), x ₁(0), x ₁(1),.; эта пропускная способность выражается формулой

Рассмотрим канал связи, на входе которого сигналы образуют стационарный процесс x ₁ = x ₁(t), M[x ₁(t)]² < ╔.

Пусть при прохождении сигнала x ₁ = x ₁(t) он подвергается линейному преобразованию Aj со спектральной характеристикой j (l) и, кроме того, на него накладывается аддитивный стационарный гауссов шум z =z (t), так что на выходе канала имеется случайный процесс x ₂(t) вида x ₂(t) = aj x ₁(t) + z (t).

Предположим также, что ограничения на входной процесс состоит в том, что M[ x ₁(t)]² ё D ² (постоянная D ² ограничивает среднюю энергию входного сигнала). Пропускная способность такого канала может быть вычислена по формуле

(в последнем выражении интегрирование ведется в пределах -p ё l ё p для дискретного времени t и в пределах -╔ <l <╔ для непрерывного t), где fz z (l) - спектральная плотность гауссова процесса z (t), функция f(l) имеет вид

а параметр q ² определяется из равенства

Нужно сказать, что если функция f(l ) представляет собой спектральную плотность регулярного стационарного гауссова процесса x ₁(t), то этот процесс, рассматриваемый как входной сигнал, обеспечивает максимальную скорость передачи информации: I(x ₁,x ₂) = C. Однако в наиболее интересных случаях, когда время t меняется непрерывно, функция f(l ) обращается в нуль на тех интервалах частот l, где уровень шума сравнительно высок (отличные от нуля значения f(l ) сосредоточены в основном на тех интервалах частот l, где уровень шума сравнительно мал), и поэтому не может служить спектральной плотностью регулярного процесса. Более того, если в качестве входного сигнала выбрать процесс x ₁(t) с спектральной плотностью f(l ), то этот сигнал будет сингулярным и соответствующая скорость передачи информации I(x ₁,x ₂) будет равна нулю, а не максимально возможному значению C, указанному выше.

Тем не менее, приведенные выражения полезны, так как позволяют приблизительно представить вид спектральной плотности f(l ) регулярного входного сигнала x ₁(t), обеспечивающей скорость передачи I(x ₁, x ₂), близкую к максимальному значению C. С практической точки зрения наиболее интересен случай, когда канал связи имеет ограниченную полосу w пропускаемых частот, т.е. когда спектральная характеристика выражается формулой

а проходящий через канал шум имеет равномерный спектр:

В этом случае пропускная способность может быть вычислена по приближенной формуле

.

При этом входной сигнал x ₁(t), обеспечивающий скорость передачи информации I(x ₁, x ₂ ), близкую к максимальной, является гауссовым стационарным процессом со спектральной плотностью f(l ) вида

так что параметры D ² и s ² имеют следующий физический смысл:

- энергетический уровень входного сигнала,

- энергетический уровень шума.

Previous: 2.9.1 Используемые стандарты    UP: 2.6 Методы сжатия информации
Down: 3 Каналы передачи данных    Next: 3 Каналы передачи данных